算法：有限状态机FSM

Leetcode 137

给你一个整数数组 nums ，除某个元素仅出现 一次 外，其余每个元素都恰出现 三次 。请你找出并返回那个只出现了一次的元素。

你必须设计并实现线性时间复杂度的算法且使用常数级空间来解决此问题。

由于 “只有一个元素出现一次， 其他都是三次”， 那么假如我们 “数” 每一个二进制位上1出现的次数， 其最终结果必定如下图所示：

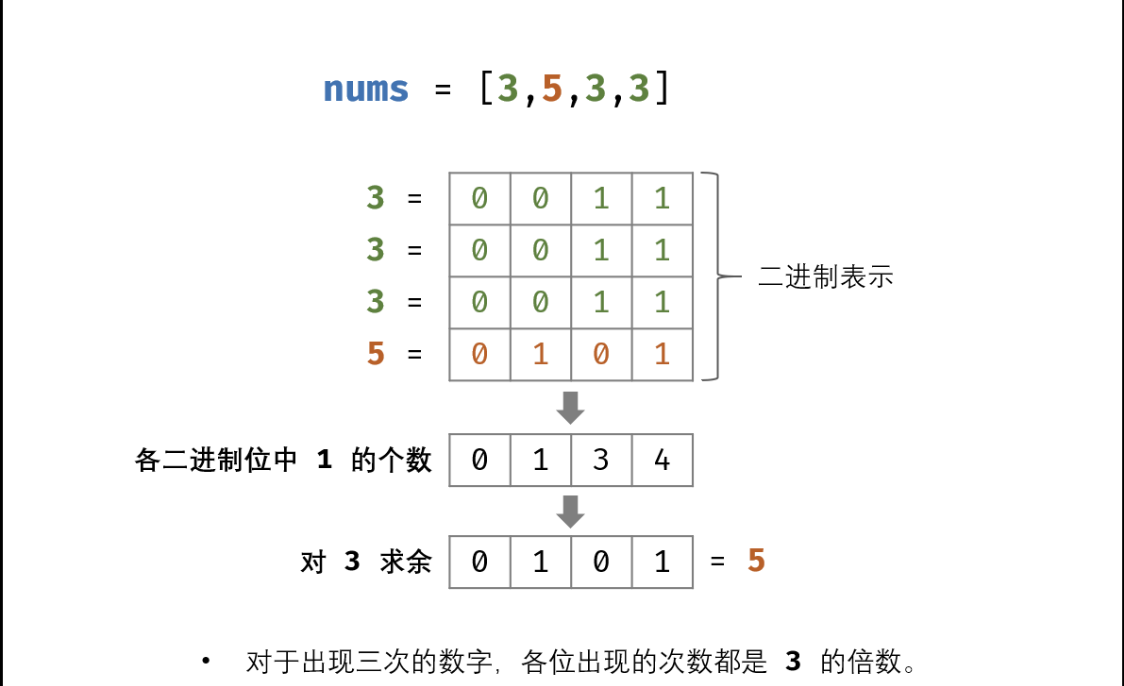
也即， 每一个二进制位上， 1 出现的次数 对 3 求余的话， 其结果 要么是 0 （即 只出现一次的 数字在这一位上是0）， 要么是 1 （即 只出现一次的数字在这一位上 是1）。

为什么？ 因为“只有一个数字出现一次， 其他数字都是三次”， 这也就意味着， 每一位上1出现的次数， 只可能是 1, 3, 4(1+3), 6, 7(1+2*3)…

那么下一步我们只需要 遍历数组， 进行计算， 得到每一位上 1 出现的次数，对3求余， 即可 得到答案。

这样当然可以， 但是我们发现一个问题。 假设以上图为例， 某一个单个 位上的 1 的个数可能很大， 假如 数组中 有 1000 个数， 这个值可能是1000. 不好表示。那么不妨我们直接在遍历过程中 计算 某一个位上 1 的个数 对3 求余的 变化， 最终得到结果。

进一步讲， 当我们遍历完所有数字， 某一个位上 1 的个数对3 的余数 只有两种可能： 1 或者 0.

但是这是遍历完以后， 在遍历过程中， 由于我们要一个一个的遍历数字， 所以在过程中 一定会出现 对3余数为2的时刻。

也即， 每一位 对于3 求余 的余数 有三种可能性： 0，1，2

由于有三种状态， 那么我们需要表示为：

00 -> 余数为0 , 01 -> 余数为1 , 10-> 余数为 2.

以这张图为例。 我们遍历数组中， 所更新的 二进制数长成这样：

00 （代表左边第一列 1 的个数对3的余数） | 00 （左边第二列）| 00 | 00

即， 对于 每一个元素的二进制数上的每一位， 我们需要维护 一个 长度为 2 的二进制数 来记录其余数的变化。

那么， 不妨将长度为 2 的二进制数拆开， 变成 高位和低位 两组 二进制数， 即：

high: 0 0 0 0

low: 0 0 0 0

此时， 对于上图中 对3 求余 的 二进制数 0101, 他实际上是 00, 01, 00, 01, —-> 拆开成 high & low:

high: 0 0 0 0

low: 0 1 0 1

不难发现， 当我们遍历完数组， 计算完 low and high以后， low所对应的值即为答案。 为什么？ 因为上面说的， 对三余数为2 的情况只是一个中间状态， 最终所有位上的1的个数 对三的余数 要么是 0， 要么是 1， 也即对应着状态 00 & 01

到这里， 我们要做的就仅仅是 遍历数组， 然后更新 high & low. 他们的状态变化为下图所示 （下图中 two代表high， one对应low， 图是偷的）：

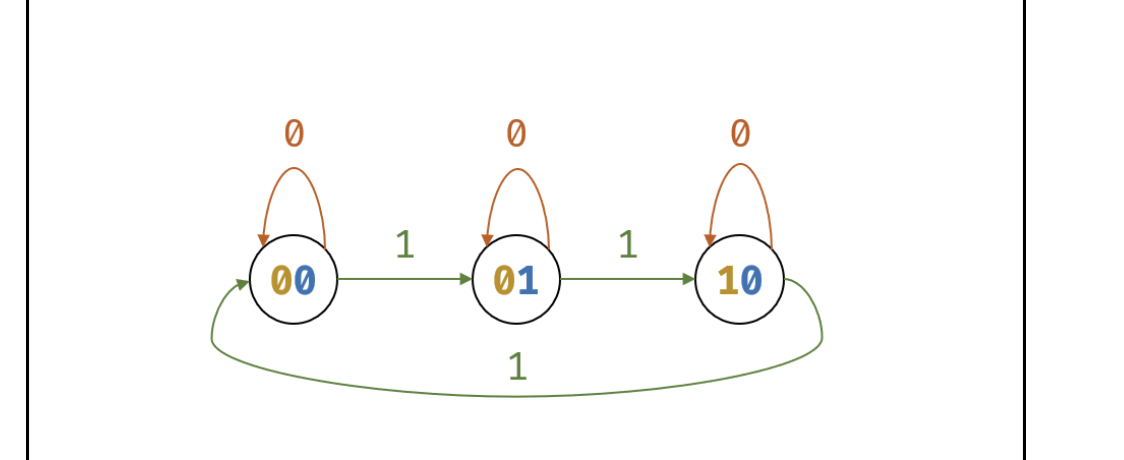
也即， 当我们遍历到数组中一个新的元素， 要计算 low中或high中某一位的值， 要取决于 high 中 或 low中 对应的值当前为多少。 为什么？ 因为low 和high是拆开的嘛， 两者何在一起才能表示当前这一位上 1 的个数对三的余数为多少。

到这里我们能得到：

if high == 0: // 看上图， 如果 橘色代表的高位是 0 时， 当遍历的数字当前位为 1， low 是要取反的， 当遍历的数字当前位为0 则不变
if n == 0:
Low = low
if n == 1:
Low = ~low
if high == 1:
Low = 0

引入 异或运算 ，可将以上拆分简化为：

if high == 0:
Low = low ^ n
if high == 1:
Low = 0
引入 与运算 ，可继续简化为：

Low = low ^ n & ~high

对于 high的计算， 也是一样的公式。

这题的重点在于理解， high 和 low两个二进制数的意义， 即他们原本应该是写成： 00 | 00 | 00 | 00 | ……

但是为了计算方便， 所以拆成了两个二进制数high和low。

其次在于理解， 为什么计算结束后， low代表的值即为答案。

最后则是理解 位运算的公式推导过程。