Two Random Algorithm

两个取随机数算法

洗牌算法

即给你一个数组， 要求你打乱这个数组。 也可应用于“扫雷这种类型， 例如 随机在数组中的几个位置生成雷”。

如何确定/验证算法所打乱的数组真的是随机的？

通过结果的可能性的数量来确定是不是真的打乱了

即， 对于一个长度为n的数组， 对其进行 全排列 的结果可能性数量为 n!。

那么只要保证算法所打乱的数组， 也有n！中可能性即可确定 算法被打乱的数组 真的被打乱了。

注意：洗牌算法目的在于‘打乱’数组， 正确性自然是通过 排列组合总数证明的！

理解以后直接看代码实现即可。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public class ShuffleAlgorithm_L384 {
    private int[] nums;
    private Random random;

    public ShuffleAlgorithm_L384(int[] nums) {
        this.random = new Random();
        this.nums = nums;
    }

    public int[] reset() {
        return this.nums;
    }

    public int[] shuffle() {
        int n = nums.length;
        int[] copy = Arrays.copyOf(nums, n);

        for (int i = 0; i < nums.length; i++) {
          	// 对于每个下标i， 其可能被交换到的下标范围为 [i, len-1], 即 n-i, where i 为下标
            // (len-1 - i + 1), +1 因为下标从0 开始
            int randomIndex = random.nextInt(i, nums.length);
            swap(copy, i, randomIndex);
        }

        return copy;
    }

    private void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }
}

局限

不难发现， 该算法只能处理 数组长度已知并且长度不变的情况 (当然也很正常， 因为这个算法的目的就是打乱一个数组)。

那么对于扫雷游戏中随机地点生成地雷这种需求， 虽然也可以利用这个算法“将地雷随机分配到某个地点”（先将x个地雷全部放到数组头部， 然后打乱数组， But what if 你不知到元素总量， you may say 我可以遍历两次数组， 第一次遍历数有多少元素， 第二次再选取， 但是如果数组长度是动态的呢？ 例如遍历了第一次数组以后， 数组长度就变化了。—> This is where reservior algorithm should be used.

蓄水池算法 Reservior Algorithm

蓄水池算法目的是“随机抽样”， 并且算法无需知道 元素总量是多少， 也无需样本数量固定。

这意味着对于streaming data, 该算法依然可以生效。

那么要证明算法选取的样本真的是随机的， 自然是证明每个样本被选择的概率都是 1/n.

算法实现

算法通过简单的数学运算实现， 首先要理解的一个point是： “假设只需选取一个元素， instead of 只选取一次， 算法会对每个元素都进行 ‘选与不选’的判断， 即 加入 1-10 是个数字中， 已经选取了1， 对于剩下的 2-9 也可能会再次选取， 只不过 如果又选到了2， 那么原本选取的 1 就不要了 ”

进而不难发现， 假设最终成为答案的样本编号为 k，那么 k 成为答案的充要条件为「在遍历到 k 时被选中」并且「遍历大于 k 的所有元素时，均没有被选择（没有覆盖 k）」 。

具体做法为：从前往后处理每个样本，每个样本成为答案的概率为 1/i （i 位样本 编号， 从1 开始）

证明

对于每一个样本 i， 由于其最终成为答案的 条件为： 「在遍历到 k 时被选中」并且「遍历大于 k 的所有元素时，均没有被选择（没有覆盖 k）」 那么其对应的概率为：

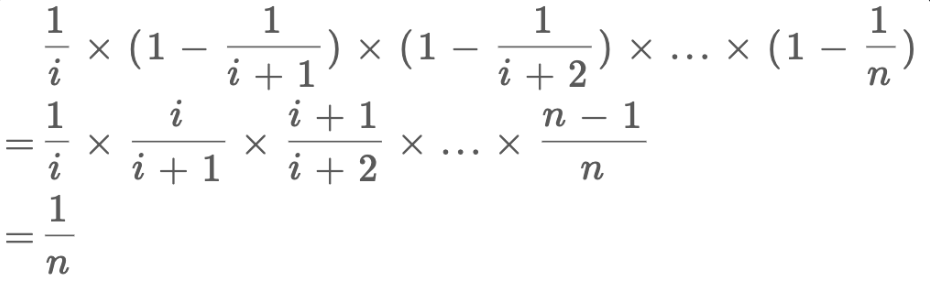
image-20230910224309928

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
public class ReservoirAlgorithm_L382 {
    private int result;
    private Random random;
    private ListNode head;

    public ReservoirAlgorithm_L382(ListNode head) {
        this.head = head;
        this.random = new Random();
    }

    public int getRandom() {
        ListNode p = this.head;
        int count = 1;

        while (p != null) {
            // radom.nextInt取值左闭右开
            if (random.nextInt(0, count) == 0) {
                this.result = p.val;
            }

            p = p.next;
            count++;
        }

        return result;
    }
}