算法笔记-回溯

Shain

2023-06-11

Algorithm › BackTrack

backtrack

回溯问题总结：

updated

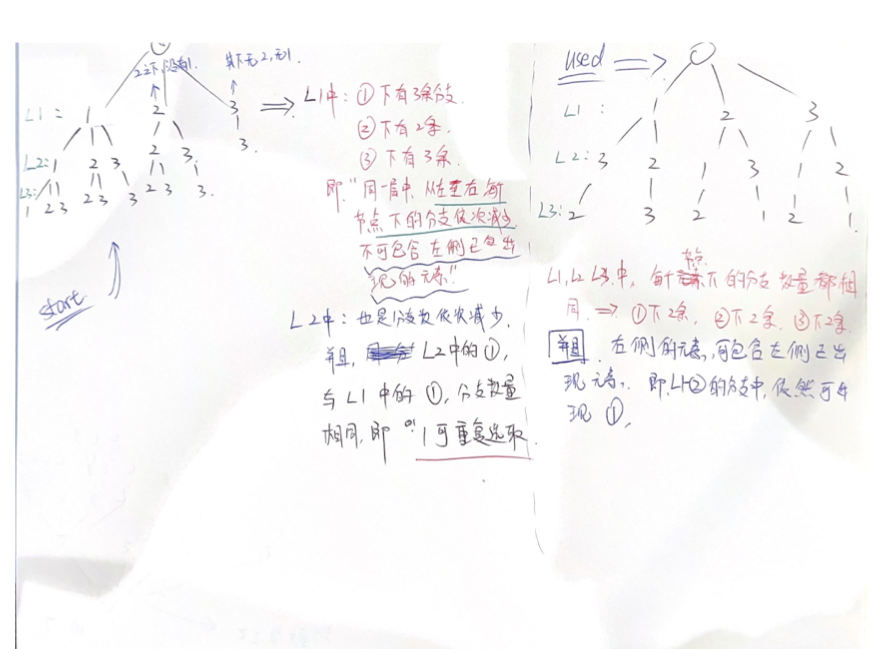
Used[] VS start

两者主要区别：

used 可使 “同一层级中，所有节点的分支数统一减少‘一定’数量”。如上图右侧部分， L1 中 1， 2， 3 下的节点均因used[] 减少了一，进而使得每个节点下的分支中，不包含自身（i.e. L1中 1 节点下的分支中不再包含 1 本身）
- p.s. 之所以说减少 ‘一定数量’，因为理论上不一定是仅仅减少1，比如，可以通过used[] 的设置，使得L1 的 1 节点下的分支中，也不包括 2。但还没遇到过这种题。

Start 主要作用仅仅是 “使得统一层级中的节点 x1, x2, x3, x4… (从左到右数， x1 在x2 的左侧， x2在x3的左侧… )，Xn 下的分支中，不包含 X1-n-1 中出现的所有元素，进而表现为同一层级中从左至右，每个节点下的分支数量依次减少”，例子如上图。

需要注意的是，一旦使用了start，必定会使得 Xn 节点下的分支中，不包括所有 X1- Xn-1 节点中的元素。即，如上图，使用了start以后， L1 的 3 节点下面，不包含1，也不包含2，只剩下了3。 “这意味着，如果你想要一个节点下的分支中不包含自己，但是要包含除了自己以外的所有元素，你需要使用 used，而不是start，因为这会使得一个节点下丢失更多的元素。” 一个例子如下：

public void backtrack(LinkedList<Integer> path, int curSum, int start){
        for (int i = start; i < candidates.length; i++) {
          	
          	// 此处i+1 确实使得当前节点下的分支中不包含自己， 但是也 排除了所有 0-i 之间的元素。
            backtrack(path, curSum, i+1);
          
        }
    }

old

无非三种情况：

同一层级中，每个节点的分支数相同。 –> 使用 used[] 改变状态，不使用 start作为递归方程的参数。
- e.g. leetcode 全排列1，2
同一层级中，每个节点的分支数不相同，即同一层级中，节点2 的分支中不包含节点1的元素，同理，节点三的分支中不包含节点1，2两个节点的元素。 –> 使用 start 作为递归方程的参数，进而改变for循环开始位置，即从start开始，即：
- e.g. leetcode 39

1 2	for i in range(start): back_track(start=i, xxx)

各层单个节点下分支数量相同，但是在单个层中，每个节点的元素数量在变化，并且输入元素的顺序不改变。语言不好理解，我想表达的是 Leetcode 93. IP地址，以及offer46 的这种类型；（offer46 应用DP求解，但bt也可以做，只不过效率低）
- 对于这种类型，格式也较为固定，代码框架如下。

def ip_config(s):
    def back_track(remained_s, ip, ip_seg, count):

        # 剪枝条件
        if .....

        # 终止条件
        if count == 1:
            ...
            
        # ！！！！重点在这个for循环， 此处， i的范围， 表示 ”单个节点内， 元素数量的可能性“
        for i in range(1, 4):
            ip_seg = remained_s[0:i] + "."
            temp = ip + ip_seg
            back_track(remained_s[i:], temp, ip_seg, count - 1)

    if len(s) < 4 or len(s) > 12:
        return []

    to_return = []
    back_track(s, "", "", 4)
    return to_return

通常， abc 不等同于 acb时，则需使用情况1，即使用used，使分支数相同。而若 abc 等同于 acb，即顺序无关，则应使用情况2，避免重复解。

之所以情况二可以避免重复解，画个树，或者举个例子即可明白。简单说， e.g. 2为最上层节点，其一条分支为 2， 2， 3；那么到了最上层的2的同级节点3以后，就不应该再在3的分支中包括2，因为这样一定会出现一条分路 3， 2， 2，进而造成重复。

More About used：

Used 的作用即为：控制单个节点下的分支个数，也即单个节点下的分支有哪些节点。比如，一个节点的分支中，应不应该有自己？此时则应用used控制，通过递归前，后的更改/还原状态控制。

注意， used和start并非不可同时使用，看情况判断。

关于求子集问题

即 offer38 的扩展题。输入123，输出： 1， 2， 3， 12， 13， 23， 123

即不仅仅输出“一条到叶子节点的路线”，也要输出第一层，第一层+第二层，第一层+ 第二层+ … + 第n层

def subset(s):
    def back_track(start, path):
      	# 载递归函数入口就将path加到result上即可。
        to_return.append(path[:])
        if start == len(s) - 1:
            return

        for i in range(start, len(s)):
            if used[i] is False:
                used[i] = True
                back_track(i, path + [s[i]])
                used[i] = False

    used = [False] * len(s)
    to_return = []
    back_track(0, [])
    return to_return

该问题相当于上文中情况1， 2的结合使用。即所说的used和start的同时使用的情况的例子。

唯一需要注意的是：这一问题的特殊点在于不仅仅输出到叶子节点的完整路线，也要输出“从第一层节点，到每一个节点的temp 路线”。实现原理很简单，在函数入口直接 append就可以。

之所以这么实现，是因为每调用一次 backtrack() , 就是向下创建了一层，到达了一个新的子节点。而此时， path中已经更新了当前这个新的叶子节点的值，那么只需要直接append path to result，就相当于实现了 “第一层节点，到每一个节点的temp 路线都被记录下来”这一目的。

如下图，每call一次 backtrack，就创建了一个新的子节点，也即一条edge。也即，要记录从第一层节点到每一层节点的路径，只需要在backtrack路口处添加path到result就可以。

复杂些的问题 - 搜索问题？

大概率从剪枝条件入手创造难度。

补充：重复元素问题

看intellij 代码注释。

L47: 通过used 排除同一层级中的重复元素。

L40: 没有used数组，只用了start，怎么排除？

首先，重复的元素在排序以后一定是 i > 0 && nums[i] == nums[i-1]

但是像 L47注释中写的，只利用这一条件跳过重复元素会错误的漏掉 “不同层级，但是val相同的节点。”

那么我们不妨看看，这些被错误漏掉的节点都是谁？上图中可发现，其实被错误漏掉的只有 L2.A 的这个1。

为什么？因为 L2.B 的这个 1 本来就属于同一层级中的相同元素，即本来就是应该被略过的。

因此，其实我们只需要保留到 L2.A 的这个1 就可以了，而这个 1 的条件是什么？ —> i == start

那么，除了这个 1 以外的 1 全部都排除，自然就能排除所有同一层级的重复元素，也即将 i==start 取反，得到 i < 0 || i > start, 而 i 又不可能小于start，所以得到：只要是 i > start, 并且 nums[i] == nums[i-1] 的元素全部是应该排除的重复元素。

问，那么 L2.c 中的2 会被正确保留吗？ –> 当然，因为对于 L2.C 这个 2，不满足 nums[i] == nums[i-1] 。